אנרגיה כימית מבוא
אנרגיה פנימית של חומר
בפרק זה נדון בנושאים הקשורים למהות ההתרחשות של התגובות הכימיות.
ננסה להסביר בקצרה מהי אנרגיה של חומר מסוים, ואיך ניתן להשוות בין כמויות אנרגיה של חומרים שונים.
בעיקר נלמד להתייחס לשינויי האנרגיה החלים בתהליכים שונים, לחשב אותם, להשוות בין שינויי האנרגיה השונים החלים בתהליכים שונים, ולראות את הקשר ביניהם.
נכיר מספר שיטות לחישוב שינויי אנרגיה. נלמד להכיר את חוקי הבסיס הקשורים לאנרגיה, בפרק הקרוי תרמודינאמיקה, ולהבין איך ניתן בעזרת חישובים תאורטיים לדעת האם תהליכים מתרחשים או לא מתרחשים.
בנוסף לכך, נלמד על קצב / מהירות התרחשות התהליכים, ועל הגורמים המשפיעים על קצב התרחשות התהליכים.
נכיר את מהותו של המושג שיווי משקל כימי, וכן תופעות הקשורות לתהליכים הקשורים להיבט זה.
אז מהי אנרגיה?
ראשית, אנרגיה שונה מהרבה מאוד גדלים אחרים, כמו מסה או נפח, שהם יותר מוחשיים לנו וקלים יותר למדידה.
ישנן הגדרות שונות לאנרגיה – היכולת לספק חום, או היכולת לבצע עבודה, או היכולת לבצע תהליכים וישנן עוד הגדרות .
כשמתייחסים לחומרים כימיים שונים ורוצים לדעת כמה אנרגיה יש להם יש להתייחס לאנרגיה הנובעת מהאינטראקציות בין החלקיקים שלהם ולאנרגיה הנובעת מהתנועה שלהם.
האנרגיה שמתייחסת לאינטראקציות בין חלקיקי החומר, מתקשרת לאנרגיה הפוטנציאלית שלו.
אילו האנרגיה הקשורה לתנועה של חלקיקי החומר מתקשרת לאנרגיה הקינטית של החומרים.
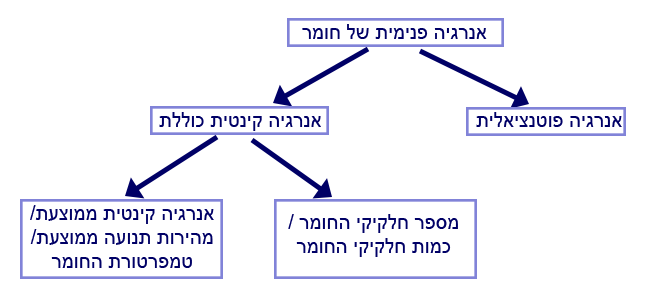
הערך הכולל של האנרגיה הפוטנציאלית והאנרגיה הקינטית הוא האנרגיה הפנימית של החומר .
בפרק זה לא נרחיב את הדיון לגבי האנרגיה הפוטנציאלית של החומר. עלינו לדעת שהיא מהווה אחד משני מרכיבים של האנרגיה הפנימית . המרכיב השני הוא האנרגיה הקינטית ועליו נרחיב כעת.
אנרגיה קינטית היא האנרגיה הקשורה לתנועתם של החלקיקים . ישנה נוסחה שבעזרתה ניתן לחשב את האנרגיה הקינטית של חלקיק:
אנו לא נחשב בפרק זה את גודל האנרגיה הקינטית ( Ek) של חלקיק מסוים, אבל נוכל להבין מהנוסחה מה משפיע על גודלה של האנרגיה הקינטית שלו.
ראשית היא תלויה במהירות החלקיק (v), ושנית היא תלויה במסה שלו (m) .
כיוון שמדובר בחלקיקים רבים בו זמנית, וחלקיקי החומר אינם נעים באותה המהירות, אנו נוהגים להתייחס למהירות הממוצעת של חלקיקי החומר. מהירות זו תלויה באנרגיה הקינטית הממוצעת של חלקיקי החומר .
ככל שהאנרגיה הקינטית הממוצעת של חלקיקי החומר גדולה יותר אז המהירות הממוצעת של חלקיקי החומר גדולה יותר ולהפך.
ככל שחלקיקי החומר זזים מהר יותר (/מהירות התנועה הממוצעת של חלקיקי החומר גדולה יותר) אז האנרגיה הקינטית הממוצעת שלהם גדולה יותר ולהפך.
הביטוי החיצוני / המקרוסקופי / הנמדד לכך שלחלקיקי החומר יש אנרגיה קינטית ממוצעת גדולה יותר (/שחלקיקי החומר בעלי מהירות תנועה ממוצעת גדולה יותר), או אנרגיה קינטית ממוצעת קטנה יותר (/שחלקיקי החומר בעלי מהירות תנועה ממוצעת קטנה יותר) הוא טמפרטורת החומר.
ככל שטמפרטורת החומר הנמדדת גבוהה יותר, לחלקיקי החומר אנרגיה קינטית ממוצעת גדולה יותר, אפשר גם לומר שחלקיקי החומר נעים במהירות ממוצעת גדולה יותר. ולהיפך ככל שטמפרטורת החומר הנמדדת קטנה יותר, לחלקיקי החומר אנרגיה קינטית ממוצעת קטנה יותר. אפשר גם לומר שחלקיקי החומר נעים במהירות ממוצעת קטנה יותר.
האנרגיה הקינטית הכוללת של החומר תלויה גם בכמות חלקיקי החומר(מספר החלקיקים). ככל שכמות חלקיקי החומר(מספר חלקיקי החומר) גדול יותר כך גם האנרגיה הקינטית הכוללת של החומר תהיה גדולה יותר ולהפך.
ניתן לסכם זאת בתרשים:
- נתונים שני כלים המכילים מסה שווה של אותו נוזל.
בכלי שבו הטמפרטורה גבוהה יותר.
שני הכלים מכילים אותה מסה של נוזל, אבל לכל חלקיק בממוצע בכלי II יש אנרגיה קינטית גדולה יותר, כי טמפרטורת הנוזל גבוהה יותר. לכן, בסה”כ האנרגיה הקינטית בכלי II גדולה יותר.
ניתן לדמות את האנרגיה הקינטית, האנרגיה הקינטית הממוצעת ומספר החלקיקים (המסה), למקרה הבא:
בשתי כיתות יש מספר זהה של תלמידים (אותה מסה), נניח 8 תלמידים בכיתה.
בכיתה ה- I יש לכל תלמיד 5 שקלים בממוצע (האנרגיה הקינטית הממוצעת); בכיתה II יש לכל תלמיד 10 שקלים (האנרגיה הקינטית הממוצעת בכיתה השנייה).
בכיתה II כמות הכסף הממוצע, המדמה את האנרגיה הקינטית הממוצעת, גדולה יותר, כי הטמפרטורה גדולה יותר, והטמפרטורה היא המדד החיצוני לאנרגיה הקינטית הממוצעת. לכן בכיתה I יש סך הכל 40 שקל (שזו האנרגיה הקינטית הכוללת בכיתה זו) ובכיתה II יש 80 שקל (שזו האנרגיה הקינטית הכוללת בכיתה זו).
ניתן לראות שבכיתה II יש יותר כסף בסך הכל (האנרגיה הקינטית הכוללת בכיתה זו גדולה יותר).
| כיתה | I | II |
| מספר ילדים (מסה) | 8 | 8 |
| כסף בממוצע (אנרגיה קינטית ממוצעת/ טמפרטורה) |
5 | 10 |
| סך כל הכסף (אנרגיה קינטית כוללת) |
40 | 80 |
- נתונים שני כלים A ו-B. בשני הכלים אותו הנוזל שנמצא בטמפרטורה של 20°C.
בכלי A יש 100 ג’ מהנוזל ובכלי B יש 50 ג’ מהנוזל.
א. באיזה כלי האנרגיה הקינטית הממוצעת גדולה יותר?
בשני הכלים אותה אנרגיה קינטית ממוצעת, כי בשני הכלים הנוזל נמצא באותה הטמפרטורה.
ב. באיזה כלי האנרגיה הקינטית הכוללת גדולה יותר?
בכלי A האנרגיה הקינטית הכוללת גדולה יותר כי בשני הכלים אותה אנרגיה הקינטית הממוצעת שווה (אותה הטמפרטורה), אבל בכלי A מספר החלקיקים / המסה גדולה יותר, ולכן סך כל האנרגיה הקינטית הכוללת בכלי זה יהיה גדול יותר.
ננסה להדגים זאת שוב עם הכסף בשתי הכיתות. הפעם בשתי הכיתות כמות הכסף הממוצע שיש לכל תלמיד שווה (נניח שלכל תלמיד יש 20 שקלים בממוצע), כי הטמפרטורה שווה, אז האנרגיה הקינטית הממוצעת שווה.
אבל מספר התלמידים (המסה) לא שווה. נניח שבכיתה A יש 10 תלמידים ובכיתה B יש 5 תלמידים ולכן:
| כיתה | A | B |
| מספר ילדים (מסה) | 10 | 5 |
| כסף בממוצע (אנרגיה קינטית ממוצעת/ טמפרטורה) |
20 | 20 |
| סך כל הכסף (אנרגיה קינטית כוללת) |
200 | 100 |
- מניחים כוס מים בטמפרטורה של 80°C על השולחן. לאחר זמן מה מודדים את הטמפרטורה בכוס והיא 40°C.
א. האם חלה עלייה או ירידה באנרגיה הקינטית הממוצעת של החומר?
חלה ירידה באנרגיה הקינטית הממוצעת של החומר כי חלה ירידה בטמפרטורת החומר.
ב. האם חלה עלייה או ירידה באנרגיה הפנימית של החומר?
חלה ירידה באנרגיה הפנימית של החומר כי חלה ירידה באנרגיה הקינטית הממוצעת של החומר ולכן חלה גם ירידה אנרגיה הקינטית הכוללת של החומר ולכן גם ירידה באנרגיה הפנימית של החומר.
נחזור בהמשך לחישובים מוערכים של האנרגיה הקינטית הכוללת של החומר, ולהערכה של האנרגיה הפנימית.